MathsConf23

For various (non-exciting, just being busy!) reasons, Twitter and blogging and MathsConfs have taken a bit of a back seat for me over the last 18 months or so – but today I attended the virtual #MathsConf23 and I feel inspired all over again. It was a busy day (6 sessions) and I have so many thoughts and questions and strategies which I cannot get to wait to try out in the classroom.

Session 1

So, my first workshop of the day was ‘Why Learning Maths is Hard…. And What We can do to Help’, by Stuart Welsh (@maths180). I’ve never seen Stuart speak before but I took so much away from his session. The title of this workshop really resonated with me – I think during my first couple of years of teaching I would frequently tell my students ‘this is easy – you’re going to understand’. This was a mistaken approach at motivating them (‘if they think it’s going to be easy, they’ll be more prepared to persevere’), but typically it had the opposite effect (‘if it’s so easy, and I still don’t understand, the problem must be me ‘).

Stuart began by drawing upon Geary’s distinction between biologically primary and secondary knowledge. Biologically primary knowledge is that which we have evolved to learn (walking, talking etc.), whereas we need to be instructed to acquire biologically secondary knowledge (how to solve a quadratic equation). This is one reason why learning Maths is difficult – acquiring any biologically secondary knowledge is hard and requires effort. What else makes learning Maths difficult? The inherently hierarchical structure of the subject means that to learn new maths, many prerequisites need to be secure already; if we try to instruct our pupils in new content when they are not secure, the new learning is likely to fail.

One of the points Stuart made that resonated most with me was that many mathematical concepts are ‘more than the sum of their constituent parts’. For example, a student could recall and use a procedure to solve an equation but there is still something beyond just the procedure that we would expect a student to possess if they really understood what it meant to solve an equation. Much of this comes back to what students are thinking about and what their attention is on – while we cannot control what our students think about, successful task design allows us to influence what they might be attending to at any moment. This is an area of my practice that I am keen to develop; although this is something that I have improved at, I am aware that I don’t expose my students as frequently to rich tasks as I could.

Another real take-away for me from this session was on problem-solving; problem-solving is something that students find hard. Students often feel overwhelmed when faced with an unfamiliar problem, and will not know where to start – something that I need to make more of an effort to do is to model problem-solving as though I am a novice. This is difficult! It’s hard to imagine being faced with a GCSE type question where I wouldn’t immediately be able to identify what area of Maths was required and select an appropriate strategy to solve. I need to do more to put myself into the position of my learners and make my thinking process more explicit.

Finally – the other distinction that Stuart drew upon what between necessary and arbitrary knowledge. Arbitrary knowledge is that which could be differently as it is often a matter of convention; names of shapes and function notation could be examples of this. This knowledge cannot be ‘discovered’/deduced – it can just be told to our students. Necessary knowledge is different; it can be deduced and reasoned about – such as the idea of why were using inverse operations to solve an equation. The problem, then, is where necessary knowledge is taught as though it is arbitrary. In doing so, maths just becomes a list of unconnected and random procedures to be memorised. This really rang true. More of my students than I would care to admit would view Maths as just lots of different things – and don’t have the bigger picture understanding of how concepts and ideas all link together and make it such a joy! I need to make this a priority.

Session 2

Next, I attended Behaving Mathematically by Jonathan Hall (@StudyMaths), who is also the creator of www.mathsbot.com. I was really looking forward to this session – as I’ve alluded to earlier, a definite tendency in my teaching is to prioritise procedural competency/fluency, and I find it easy to neglect providing my students with sufficient opportunities to practice thinking and behaving mathematically.

Jonny opened with this quote:

Now, I couldn’t agree with this more – I would always articulate my aims for my students in a similar way, and yet I know I don’t think this is what is happening in my classroom (at least, to the extent which I would like it to).

The session focused upon prime factorisation; this is an area of Maths that I do really enjoy teaching and I think it’s something I’ve improved my delivery of. I am aware that prime factorisation can be viewed by students as ‘just another procedure to memorise’, and so I was keen to explore ways to prevent this.

Jonny began by showing us prime factorisation tiles – I’ve been aware of these for a while but had no idea of how to effectively use them in the classroom. It would be hard to do justice to the session in this post, but I was really struck by how fun and joyful the entire session was. We looked at a sequence of questions (express 300 as a product of prime factors, express 600 as a product of prime factors etc.) which wouldn’t be dissimilar to a sequence I would use, but the addition of the physical manipulatives made the experience just feel so different.

Moreover, the tiles led much more intuitively to the idea of using the prime factorisation of two numbers to find their Highest Common Factor and Lowest Common Multiple. I have generally opted for the Venn Diagram method in the past; while this generally works well and most students can be successful with it, I am not convinced that enough of my students understand the underlying structure of the mathematics. I particularly loved how straightforward the tiles made it to find all possible factors of a number, in a systematic way.

The session closed with a couple of real ‘wow’ moments! I don’t want to say too much more as I think it would be far more worthwhile to catch up with the session yourself. Honestly – I was so amazed and I am buzzing about the possibility of using some of the tasks Jonny suggested in my classroom. The tasks provide students with the opportunity to specialise, generalise and conjecture – which are the constituent parts of what it means to behave mathematically. Ultimately, being in this session for me was the way I would want students to feel when they are in my lessons – I cannot recommend catching up with it more highly.

 

Session 3

For session 3 I was meant to be attending ‘Pi vs. Tau and other Mathematical Arguments’ with Ayliean McDonald (@Ayliean). Disappointingly, this session was cancelled due to technical issues and so I am hopeful that I will still get to attend this workshop on a future date. However, I went along to ‘Working with Low Attaining Pupils’ with Gary Lamb (@garyl2). I did miss the beginning of the session and so I am glad I will get to catch up with it!

Gary made the point that a mastery approach to learning does not mean that we should solely focus down on tiny aspects of procedures – to do so is reductionist. A really interesting quote from Guskey (1997) was shared: ‘some students are good at guessing what they are expected to learn, many others are not. For those who are not, learning soon becomes a frustrating experience.’ This really resonated with my experience within the classroom.

Similarly to session one, the idea of ‘what is it like to be a novice?’ kept recurring throughout this session. In many ways, I am a terrible novice learner. I don’t come from a particularly Maths-y background, and my degree isn’t in Maths, and so something I do intermittently is to try and learn some Further Maths A Level. Although I am enjoying the experience, it’s still true that I find it hard and frustrating and I really struggle to ask for help. I don’t like people looking at my work unless I am certain that it is right: it is something I just find quite stressful. Yet, when I am in the classroom and in my comfort zone I forget that this is what it can be like to be a student. I expect them to be as excited as me about solving equations or using Pythagoras’ Theorem – which is an unfair expectation. I have so much to think about here.

The workshop also looked at the relationship between motivation and achievement. Gary made the point that motivation needs to be built through achievement; I think this is incredibly important, and that trying to develop motivation where achievement isn’t there is never likely to yield positive results. The importance of sincere praise should not be underestimated here; by praising the specific mathematical behaviours we want to see (‘well done, I know you found that problem challenging but you looked back in your work to find a similar example which you used to help get started – that’s fantastic!’), we are more likely to see a repetition of those behaviours in the future. This is particularly important for our lowest attaining students.

Gary also highlighted the importance of alternating examples and problems within our teaching, and shared some research which suggested that this leads to the greatest long-term gains. He made the point that with a typical example-problem pair, a student can follow the steps during an example, but forget those steps when faced with a similar problem. By introducing additional scaffolding (in the form of naming the steps or allowing pupils to ‘trace the mathematics’) we increase the probability of all students being successful. Over time (and this is why patience is key!), these scaffolds can gradually be removed.

The final takeaway for me from this session was Gary’s point about overlearning. I think it is perhaps easier with our lowest attaining students to provide them with more repetitive practice, with the hope that this will means they can be successful, leading to greater confidence and (hopefully) long-term retention. However, there is little evidence to suggest that this approach is effective – ‘practice shouldn’t just be more of the same’. Gary shared a structure of ‘Do, Think, Fix’ which has been really useful for me to think about. I know that I am guilty of prioritising the ‘Do’ stage when working with lower attaining students; this is mistaken as all students need the opportunity to Think and to Fix if they are to be truly successful in Mathematics.

Session 4

For my fourth session, I went along to ‘Always Teach ‘What’ before ‘Why’’ by Kris Boulton (@kris_boulton).  I’ve seen Kris speak quite a few times before (and was lucky enough to spend a week at King Solomon Academy when he was teaching there); I know how deeply he thinks, and so I was looking forward to this workshop.

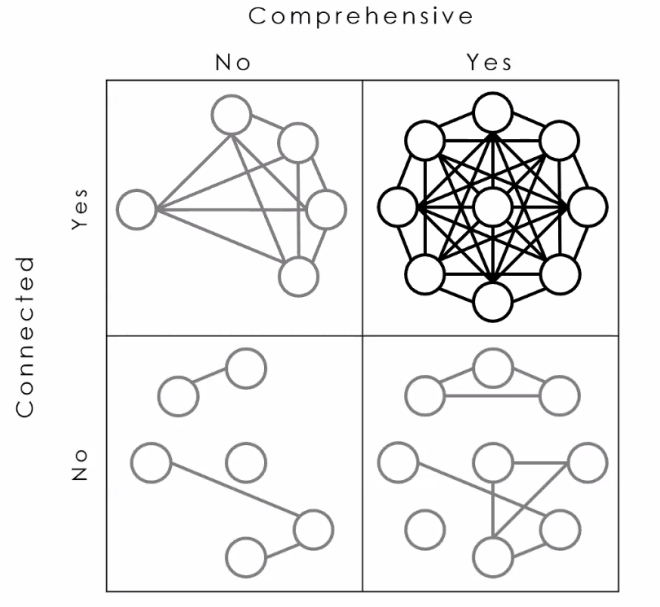
Kris shared this model of ‘understanding’. To improve students’ understanding of a given area of mathematics, we would want to increase both the quantity of knowledge they have access to and the connections between them. The top right quadrant, then, is what we are aiming for. So far, this felt relatively uncontroversial!

Kris shared his own experience of his first year or two of teaching: in his efforts to expose his students to the wonderful connections in maths, he would often try to teach everything in one go. This felt very similar to my own experience. Now, though, he would recommend teaching one thing at a time; subsequent topics should be taught on topic of that existing knowledge and connections should be built that way.

A specific example Kris gave of this was teaching students how to simplify with index notation. The approach outlined is one that I have used myself:

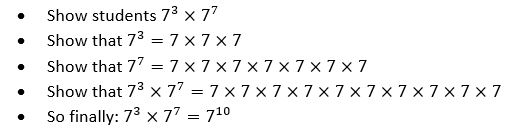
After running through several similar examples, he would introduce students to the general form (a^m * a^n= a^m+n), before students would complete some practice. Now, while specifics may vary, I think the approach here is almost certainly the most standard approach used in classrooms today. As I say, I’ve used it myself and it feels like a reasonable approach to take. What could the problems be, then?

Kris highlighted three main problems with this type of approach. Firstly – for at least some students this is likely to induce cognitive overload. This resonated. I can think of particular students who after (what I thought was) an excellent and clear explanation would be completely overwhelmed; upon pointing out that that we just need to ‘add the powers’, everything fell into place. It also has the problem of how we ask students to practise the why – do they need to practise they ‘why’ stage in order to have understood? Moreover – when we return to this topic (as part of revision or in some other context), we do not practise the why. Finally, the journey from the start of teaching to the point where students have ‘understood’ is often long and meandering – and above all, only really interesting if you know the destination.

This final point made a lot of sense to me. Several years ago, when teaching a sequence of lessons on how to find the area of 2D shapes, I arrived at ‘area of trapeziums’. I was very keen for my students to understand where comes from, and so came prepared with several different methods of how to derive this formula. For various reasons, it was very unsuccessful and it created unnecessary confusion. Students found the derivations of the formula challenging – when they actually went on to practise finding the area, they were confused: ‘why is this bit of easy when everything earlier didn’t make any sense?’. However, I think there was something going on beyond that. I can’t especially remember when I first learnt the area of a trapezium formula. I feel reasonably confident that one of my maths teachers would have shown us why it worked at some stage, but I have no recollection of this. As such, when I started preparing to teach area of a trapezium I was so excited about all of the different ways that I could show why the formula worked. I can’t help thinking that I was only excited because I already knew what the formula was – once the ‘what’ is established as fact, the ‘why’ becomes more interesting.

For that reason, there are a couple of topics that I now teach ‘back to front’ – area of a trapezium is one of them, as is the quadratic formula. Honestly – one of my favourite all-time lessons was with my year 10 class earlier this year. I made a really big thing that we wouldn’t be looking at why this formula worked just yet – we were just going to trust that it did and get on with it. I did promise them that I would show them why, but only when I thought they were ready. This intrigued them, and they kept asking and they kept asking. Finally, I ‘gave in’ one Friday and we went through the proof of the quadratic formula and it was just magical. I’m not prone to being overly sentimental but to see it all come together for them was such a wonderful moment. Anyway, I say all this to make the point that in many ways I am onboard with teaching ‘what’ first and ‘why’ second.

Back to Kris’ workshop: Kris then went through a sequence of instruction he would now use to introduce simplifying with indices. This sequence involved starting by showing students a true statement (e.g. 7^3 * 7^7 = 7^10 ) and then changing just one thing at a time. Pupils will work through questions using mini-whiteboards. He made the point that this is a rapid process – by changing (for example) just the base number, pupils only have to change one thing on their whiteboards. It is a process that all pupils can be successful with.

I don’t want to go through the entire sequence here (honestly, catch up with the workshop!) but there were a couple of moments I particularly liked. One was the use of the question ‘193^40 * 193^7’ – Kris made the point that to students this will look difficult – and so guaranteeing their success with difficult questions will lead to increased self-efficacy. I also really liked the introduction of multiplying three terms (e.g. 2^5 * 2^8 * 2^3). With careful narration (‘I know I haven’t shown you how to do this yet, but I’m pretty confident that if you have a guess then that guess is likely to be correct’), pupils are able to make correct inferences for themselves – again, I think this can only be a good thing.

Up to this point, I was fully onboard with Kris’ ideas. However, title of the workshop was ‘Always Teach ‘What’ before ‘Why’’. This idea of ‘Always’ seemed dubious.

Kris then shared how he would now introduce students to solving quadratic equations. Rather than beginning with a quadratic equation in expanded form and asking pupils to factorise, he would begin with a quadratic equation in its factorised form. This seemed perfectly reasonable. At this point, Kris shared the example below, with the commentary ‘flip the sign, put it over this number’.

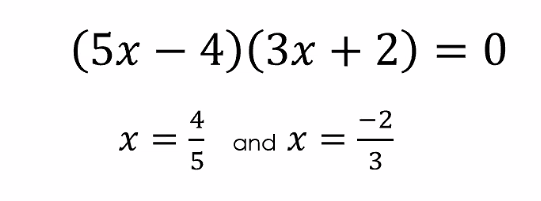
I cannot explain just how taken aback I was by this: ‘you CAN’T just say ‘flip the sign’, pupils won’t understand what they’re doing at all, this is unbelievable.’ This felt very much like a trick to show students – they might be able to do the trick but they won’t understand at all, so the ‘trick’ must be wrong.

The above slide has been shared on Twitter quite a lot (on this, I am genuinely always so impressed by the way in which Kris engages in meaningful debates), and I think without context it is easy to respond in horror (as I did!) and discount the whole thing. However – I really want to stress that Kris was not saying that we should teach pupils this and then consider that ‘solving quadratic equations’ can be ticked off the list. Once pupils are secure with this stage, they will then return to why it is working and what those missing steps are etc.

I am still very unconvinced – but I can’t really articulate why. I think much of my discomfort can be attributed to biases and currently held convictions about the ‘best’ ways of teaching Maths. I am not sure that it is best to always teach ‘what’ before ‘why’ – I think for many things the two go hand-in-hand. Above all, though, it was so valuable to be challenged and to think hard and to confront existing beliefs. I may not be about to revolutionise my teaching of solving quadratic equations but I will continue to puzzle over things and try some new things out and see what works.

Session 5

After lunch, it was time for ‘Teaching Exact Trig Values’ with Jo Morgan (@mathsjem), who is creator of the incredible www.resourceaholic.com. Jo’s sessions are always fantastic – they are filled with resources and practical strategies of things to try out. Jo began by providing some background to the topic. With the ‘old GCSE’ in Maths, trigonometry was only assessed at Higher and Intermediate tier, whereas the introduction of the ‘new GCSE’ (which is no longer that new!) meant that all students could be assessed on trigonometry, including at Foundation tier. Jo made the point that the specification says that students must know the exact trig values, but not necessarily ‘use’ or ‘apply’ them. It is worth being aware of this distinction!

There is, of course, an argument about whether exact trigonometric values should be included as part of the GCSE. For the most part, I am glad they are. I think they offer a really nice opportunity to ensure that students’ understanding of trigonometry goes beyond a set of procedures to be memorised. Moreover, for students who are going onto study Maths and Further Maths at A Level, it makes sense for them to already be familiar with these exact values. However, I am still spectacularly unconvinced for the need for exact trig values to appear at Foundation Tier. I think it is very much an example of the ‘wrong maths’ to be teaching Foundation students – and it becomes an exercise in pure memorisation as opposed to anything deeper.

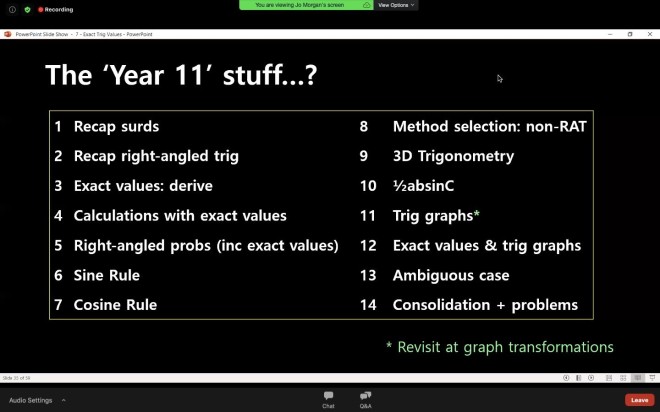
Jo shared the above as a proposed structure for how to order the teaching of ‘advanced trigonometry’. This has given me a lot to think about! Typically, I would teach sine and cosine rule before introducing exact values/non-calculator trigonometry. A more effective, approach, however, could be to introduce exact trig values earlier in the learning journey; thus, creating more opportunities for interleaving and (hopefully) attaching more meaning to these exact values. The importance of ensuring that students are fluent with surds before delving into exact values is something that Jo emphasized. This is very true; I can remember one occasion when I tried to introduce this to a class who should have been confident with manipulating surds. They were not. As such, I had to spend the lesson dealing with any number of surds misconceptions which meant that the exact trig values were lost in the surrounding noise.

I really enjoyed thinking about how to teach this topic, and also about how to ensure that students have memorised the values! Like many Maths teachers, I would always refer back to the ‘special triangles’ and encourage students to derive them as opposed to simply memorising. However, if students can gain 1 mark for recalling that , then perhaps it is worth spending more time on memorising a list. I feel deeply uncomfortable with promoting the finger trick or similar, but I need to consider if I have grounds to feel this uncomfortable. I am not sure!

My main takeaway from this session was to use exact trig values throughout all my teaching of trigonometry as much as possible. Jo shared all sorts of excellent resources to help with this (particularly from Don Steward, MathsPad and the Level 2 Further Maths qualification from AQA).

Session 6

Final session of the day now – ‘Misconceptions in Mathematics: Angles’ with Craig Barton (@MrBartonMaths). I’ll be honest: angles is not one of my favourite topics to teach. One of the reasons for this is that I think practice of basic angle properties tends either to be routine (and thus just become arithmetic practice) or increases significantly in difficulty. At this stage, some students will have become overwhelmed by the increased level of demand and I’m not as successful at helping them to bridge that gap as I would like to be.

Craig shared several questions from his Diagnostic Questions website (www.diagnosticquestions.com) – we were invited to guess what the most popular wrong answer would be. Before we even delve into any specifics, this was fascinating and something I’d like to try with our department! I would have imagined that a (virtual) roomful of Maths teachers would be extremely successful with identifying the most common misconceptions, but the results would show otherwise. It’s really interesting to think about why that might be.

One question I particularly enjoyed thinking about is this:

Students tend to opt for B, C and D in roughly equal proportions, with C just being the most popular misconception. Why might this be? There’s various reasons, but I was particularly interested in this student’s response.

This has really made me wonder: to what extent do my students do view Maths questions as needing to reach a numerical answer? I’d like to think that my students would be able to reason about the remaining angles being acute and obtuse, but then I also think that needing to ‘get to the answer’ would lead some drawn to C. I mightbe wrong, and I will need to assess this more carefully in fiuture, but if my intuitions are correct then I need to more actively cultivate a culture of reasoning, not answers, in my classroom.

I would really recommend catching up with this session and see how you do. I’m not going to go through each question here but rather discuss some of the implications of these misconceptions for how we might approach the teaching of angles.

The most important thing that I took away from this workshop was ‘include the unusual’ from the start. There are several ‘standard’ triangles in terms of orientation etc. that we tend model to our students – I rarely actively include triangles with obtuse angles, for example. This is a problem, and something that I need to actively address. Craig also highlighted the use of Intelligent Practice when introducing students to angle properties. I’m excited to explore using Geogebra to show students more explicitly the effects that changing just one thing has on the remaining angles. Finally – we need to go deep from the start. I’ve been exploring Don Steward’s Median blog (www.donsteward.blogspot.com) to find some nice resources for this:

Look at how fun this question is! It is a lovely opportunity for students to go deep and to be challenged.

Finally, I will be thinking a lot about my choice of language when teaching angles next time. The most obvious example which springs to mind is ‘angles on a straight line add to 180°’. While this is not untrue, it is full of vagueness and ambiguity, which is unhelpful to novice learners. Is at as unhelpful as ‘two negatives make a positive’? I don’t know. Maybe. Craig suggested several possible alternatives:  maybe ‘angles that form a straight line add to 180°’ or ‘adjacent angles on a straight line add to 180°’. I can’t imagine that this change in language alone will have a significant impact on students’ understanding, but I think it is likely to positively affect at least some students. This can only be a good thing.

Final Thoughts

As ever, #MathsConf23 was the most incredible day of CPD. Every single session left me thinking hard about my own practice; I have so much to reflect on. I enjoyed the virtual nature of the conference more than I thought I might, and while I am excited to see MathsConf friends at the next in-person conference, I am so impressed by how well the whole of the La Salle Education teams put together such a well-run day for so many attendees in such a short time. I am extremely glad that the conference presentations will be available to watch after. The six sessions that I attended are only a small part of the entire conference, and it’s often incredible difficult to select sessions as many similarly amazing workshops will be happening simultaneously. I would strongly recommend each of the workshops above, but I have a list to catch up with now. A huge thank-you to all of the presenters, Mark McCourt (@EMathsUK) and La Salle Education (@LaSalleEd) for the most fantastic day.